The Trigonometric Transformation
The sine trig identities
\sin(x+y) = \sin(x)\cos(y)+\cos(x)\sin(y)
\sin(x-y) = \sin(x)\cos(y)-\cos(x)\sin(y)
hence
\sin(x+y)+\sin(x-y) = 2\sin(x)\cos(y)
If we take \sin(x) as the function f(x), and y as a constant \Delta\theta, we have
f(x+\Delta\theta)+f(x-\Delta\theta)=2\cos(\Delta\theta)\cdot f(x)
or
f(x+\Delta\theta)=2\cos(\Delta\theta)\cdot f(x)-f(x-\Delta\theta)
Thus, there’s an fixed relationship between f(x-\Delta\theta), f(x) and f(x+\Delta\theta).
Discrete Sine Wave Sequence
General Form
By defining a_n = f(n\cdot\Delta\theta), we have a discrete recursive formula of sine wave
a_n = 2\cos(\Delta\theta)a_{n-1}-a_{n-2}
Let \Delta\theta=2\pi/N, there’s N of a_i in the range [0,\ 2\pi).
Moreover, if we write a_n as
a_n=k\ a_{n-1}-a_{n-2}, for any k\in (-1,\ 0) \bigcap (0,\ 1) and | a_{n-1} | + | a_{n-2} | \neq 0, a_n is always a sine sequence. This is for the reason that, for any valid k, there’s always a (or two) \Delta\theta will satisfy 2\cos(\Delta\theta)=k.
Another General Form
We can define another sequence b_n from a_n as
b_n = \cfrac{k_\mathrm{L}\ a_{n} + k_\mathrm{R}\ a_{n+M}}{k_\mathrm{L}+k_\mathrm{R}}
For any | k_\mathrm{L} | + | k_\mathrm{R} | \neq 0 and k_\mathrm{L}+k_\mathrm{R}\neq 0. The b_n is also a discrete sequence of sine wave. That’s because the following recursive formula is satisfied.
b_n=k\ b_{n-1}-b_{n-2}
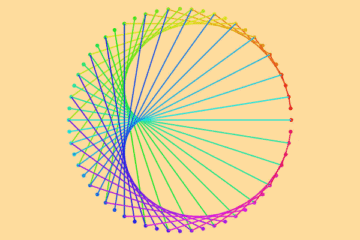
Graphical Illustration
By letting N, M, k_\mathrm{L} and k_R have different values, we can have different patterns of a_n and b_n. As shown in the figures below, a_n is the dots in black, b_n is the dots in color.
Note that: The straight line in the Cartesian coordinate system (left) is not corresponding to the straight line in the Polar coordinate system (right).
N=10, KL=1, KR=1, M varies
N=100, KL=1, KR=1, M varies
N=10, M=2, KR=1, KL varies
N=100, M=38, KR=1, KL varies
0 Comments