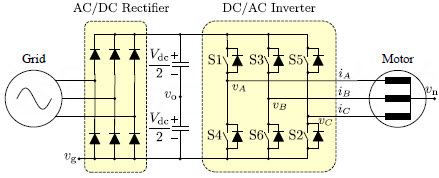
For the three-phase PWM inverter, there are three commonly used coefficients to indicate the DC voltage utilization level, i.e.
Modulation Level (调制度)
M = \cfrac{V_R}{V_T}where V_R is the magnitude (note, not fundamental amplitude) of modulation wave, V_T is the magnitude of carrier wave.
When M \leq 1, there is no distortion in the output. While M > 1 means the output is distorted from the modulation wave.
DC Voltage Utilization Ratio (直流电压利用率)
M_u = \cfrac{V_{\rm 1max}} {V_{\rm dc}}where V_{\rm dc} is the DC voltage. For single phase output application, V_{\rm 1max} is the maximum amplitude of phase fundamental voltage. For three phase output application, V_{\rm 1max} is the maximum amplitude of line-line fundamental voltage.
For single phase SPWM, the maximum M before distortion is M=1. At M=1, the amplitude of fundamental voltage is V_{\rm dc}/2, thus the DC voltage utilization ratio M_{u \rm\ 1-Phase\ SPWM}=1/2.
For three phase SPWM, the maximum M before distortion is M=1. At M=1, the amplitude of fundamental voltage is \sqrt{3}V_{\rm dc}/2, thus the DC voltage utilization ratio M_{u \rm\ 3-Phase\ SPWM}=\sqrt{3}/2.
In order to Increase the M_u of three-phase Y-connected motor, the third-order harmonic can be added to the SPWM, named as THIPWM. When the amplitude of third-order harmonic is 1/6 of the SPWM, the method is named as THIPWM1/6, as shown below.
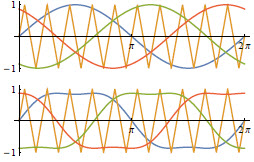
The modulation wave magnitude of THIPWM1/6 is \sqrt{3}/2 of the SPWM. Thus, when M=1, the M_u of THIPWM1/6 is 2/\sqrt{3} of SPWM. Consequently, the DC voltage utilization ratio of THIPWM1/6 M_{u\rm\ 3-Phase\ THIPWM1/6} = 1.
Also, for SVPWM the DC voltage utilization ratio is the same as THIPWM1/6, thus M_{u\rm\ 3-Phase\ SVPWM} = 1
Modulation Index (调制系数) or Voltage Utilization Level
M_i = \cfrac{V_{1\rm max}}{V_{1\rm max\ 6-step}}where {V_{1\rm max\ 6-step}} is the amplitude of the fundamental voltage (the green line below) of square form modulation wave (the blue line below) with M=1.
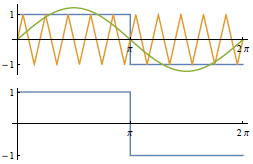
The fundamental wave of the square wave has the formula 4\sin{\theta}/\pi, thus
V_{\rm 1max\ 6-step}=\cfrac{4}{\pi}\cfrac{V_{\rm dc}}{2}=\cfrac{2}{\pi}V_{\rm dc}.
Then,
M_i = \cfrac{\pi}{2}\cfrac{V_{\rm 1max}}{V_{\rm dc}}
or,
V_{\rm 1max}=\cfrac{2V_{\rm dc}}{\pi}M_i
Consequently, for three-phase SPWM with M=1, the M_i is
M_{i\ \rm 3-Phase\ SPWM}=\cfrac{\pi}{2}\cfrac{1}{V_{\rm dc}}\cdot \cfrac{V_{\rm dc}}{2}=\cfrac{\pi}{4}\approx0.785
For three-phase THIPWM1/6 and SVPWM with M=1, the M_i is
M_{i\ \rm 3-Phase\ THIPWM1/6}=M_{i\ \rm 3-Phase\ SVPWM}=\cfrac{\pi}{4}\cfrac{2}{\sqrt{3}}=\cfrac{\pi}{2\sqrt{3}}\approx0.907
0 Comments